Question bonus à 1 point
sur la prochaine interro :
(pour la première bonne réponse)
Question 1
 |
|
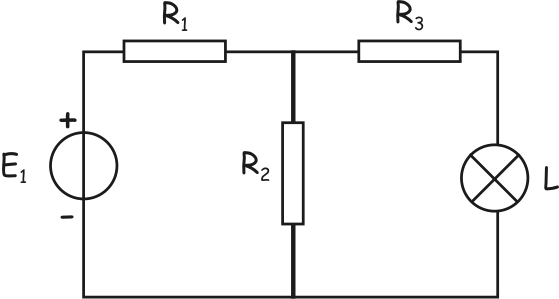
Soit le montage représenté
ci-contre.
On donne E = 6V, UR2
= 2 V, R1 = 4 Ohms, R2 = 2,5 Ohms , R3 = 2,5
Ohms.
Calculer la puissance
absorbée par la lampe.
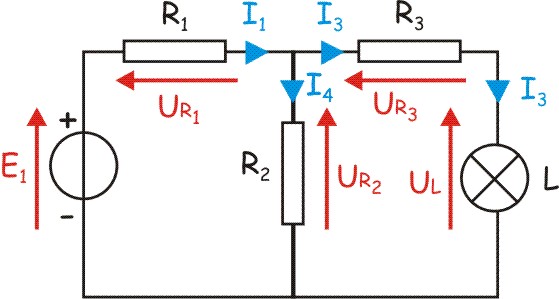
On calcule d'abord UR1 : (Loi de la maille de
gauche)
E - UR1 - UR2 = 0 d'où UR1 = E - UR2
= 6 - 2 = 4 V
puis on calcul l'intensité du courant dans R1 (loi d'Ohm):
UR1 =R1 I1 d'où I1 = UR1
/ R1 = 4 / 4 = 1 A
On peut aussi calculer l'intensité pour R2 (loi d'Ohm):
UR2 = R2 I2 d'où I2 = UR2
/ R2 = 2 / 2.5 = 0,8 A
La loi des noeuds donne alors :
I1 - I2 - I3 = 0 soit I3 = I1
- I2 = 1 - 0,8 = 0,2 A
puis on calcule UR3 (loi d'Ohm) :
UR3 = R3 I3 = 2,5 . 0,2 = 0,5 V
On en déduit UL (Loi de la grande maille) :
E - UR1 - UR3 -UL = 0 donc UL = E -
UR1 - UR3 = 6 - 4 - 0,5 = 1,5 V
Finalement la puissance qu'absorbe la lampe vaut
P = UL I3 = 1,5 . 0,2 = 0.3 W
|
Réponse
donnée par David WASILEWSKI le 10 octobre à 20h03 (1 point de bonus sur l'interro
2).
David est hors-jeu jusqu'au 21 octobre.
Question 2
Un
dipôle actif linéaire D présente une tension à vide de 9 V et une résistance
interne de 20 Ohms. Ce dipôle alimente une varistance sont le comportement
courant-tension répond à la relation I = k U² avec k = 4,2.10-3
A/V². Calculer la puissance dissipée par cette varistance.
La varistance, qui est un dipôle
passif, est récepteur, et l'équation de sa caractéristique est IV
= k UV².
La varistance étant récepteur, le dipôle actif linéaire
est générateur, l'équation de sa caractéristique électriques est donc UD
= E - r ID.
Connecté aux bornes l'un de l'autre,
les deux dipôles sont soumis à la même intensité et présente la même tension à
leurs bornes :
U = UV = UD et I
= IV = ID donc U = E - r I = E - r ( k U² )
On obtient une équation du second
degré U = E - r k U² soit - r k U² - U + E = 0 ( a = - r k ; b =
-1 et c = E )
Delta = b² - 4 a c = ( -1 )² - 4 ( - r
k ) ( E ) = 1 - 4 ( - 20 x 4,2.10-3 ) ( 9 ) = 4,024 = 2,01²
1ère solution : U1 = ( - b
- VDelta ) / 2 a = ( - (-1) + 2,01) / 2 ( -20 x 4,2.10-3 ) solution
négative à ne pas retenir !
2e solution : U2 =
( - b + VDelta ) / 2 a = ( - (-1) - 2,01) / 2 ( -20 x 4,2.10-3 ) =
6 V solution à garder.
Pour U = 6 V, I = k U² = 4,2.10-3
x 6² = 0,152 A
Finalement, la varistance absorbe une
puissance P = U I = 6 x 0,152 = 0,91 W
Réponse
donnée par David WASILEWSKI le 6 décembre à 10h54 (1 point de bonus sur l'interro
4).
David est hors-jeu jusqu'au 17 décembre.
Question 3
|
 |
|
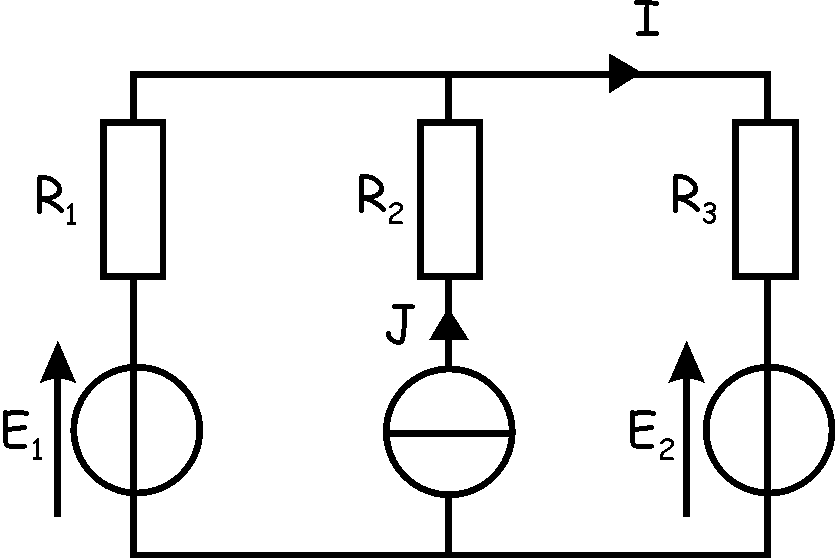
Soit le montage ci-contre.
On donne E1 = 12
V; E2 = 5 V; J = 1,5 A, R1 = 8 Ohms, R2 = 2 Ohms , R3
= 4
Ohms.
Le montage comportant
plusieurs sources, il est judicieux ici d'utiliser le principe de superposition.
(On a le droit, vu que tous les dipôles sont linéaires).
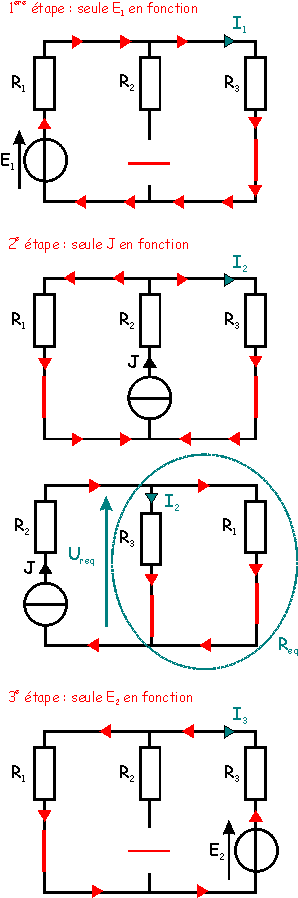
1ère étape :
seule E1 est en fonction :
Dans ce cas, le courant
circule dans la grande boucle, R1 et R3 sont en série. La
loi de la grande maille donne E1 = UR1 + UR3 =
R1I1 + R3I1 = ( R1 + R3
) I1
soit I1 = E1
/ ( R1 + R3 ) = 12 / ( 8 + 4 ) = 1 A. On trouve I1
= 1 A.
2e étape : seule
J est en fonction :
Dans ce cas, le courant J se
sépare en deux après R2 pour traverser R1 et R3
Donc J > I2 ! Nous remarquons que R1 et R3 sont
en parallèle et peuvent être regroupées en une résistance équivalente Req.
Req = 1 / ( 1 /
R1 +1/ R3 ) = 1 / ( 1 / 8 + 1 / 4 ) = 2,66 Ohms.
Nous pouvons calculer UReq
= Req J = 2,66 x 1,5 = 4 V.
Nous pouvons remarquer que UReq
se retrouve aux bornes de R3 et donc écrire UReq = R3 I2.
Finalement, I2 =
UReq / R3 = 4 / 4 = 1 A. On trouve I2 = 1 A.
3e étape : seule
E2 est en fonction :
Dans ce cas, le courant
circule dans la grande boucle, R1 et R3 sont en série.
Cependant, il faut noter que le courant délivré par E2 (appelons le
I3', ce courant est représenté en rouge sur la figure) est de sens contraire à
celui cherché, c'est à dire I3. Nous devrons donc adapter le signe à
la fin du calcul.
La loi de la grande maille
donne E2 = UR1 + UR3 = R1I3'
+ R3I3' = ( R1 + R3 ) I3'.
soit I3' = E2
/ ( R1 + R3 ) = 5 / ( 8 + 4 ) = 0,416 A.
Comme I3 = - I3',
on trouve I3 = -0,416 A.
4e étape :
application de la superposition :
Quand les trois sources
fonctionnement simultanément, on obtient :
I = I1 + I2
+ I3 = 1 + 1 - 0,416 = 1,58 A. I = 1,58 A.
|
Réponse
donnée par François RUDOWSKI le 12 décembre à 19h37 (1 point de bonus sur l'interro
5).
François est hors-jeu jusqu'au 23 décembre.
Question 4
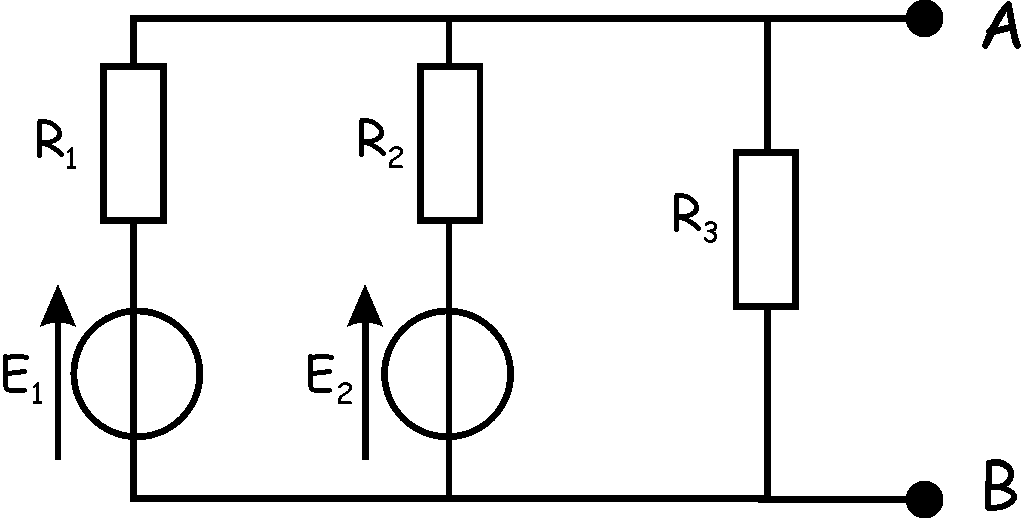
|
|
On donne E1 = 12
V; E2 = 4 V; R1 = 10 Ohms; R2 = 20 Ohms; R3
= 60
Ohms.
Le dipôle AB ci-contre alimente un dipôle D
dont la caractéristique répond à la loi U = ( 1 + 1,4 I² ). Quelle est la
puissance dissipée dans ce dipôle ?
|
Réponse à envoyer à l'adresse suivante : ascdl@chez.com
__________________________________________________________________________________________________________
Questions bonus de
l'année dernière
__________________________________________________________________________________________________________
Question 1
Un
dipôle actif linéaire D (de tension à vide 100 V et d'intensité de courant de
court-circuit de 5 A) alimente une résistance R de 10 Ohms.
Quelles sont les valeurs de la tension et de l'intensité qui traverse cette
résistance ?
Le dipôle D est linéaire,
donc sa caractéristique est une droite qui passe par les points de coordonnées
(U=E= 100 V pour I=0 A) et (U=0 pour I=ICC=5A).
La
résistance R (dipôle passif linéaire) a pour caractéristique une droite qui
passe par l'origine du repère et un point tel que U=RI (U=50 V pour I=5 A par
exemple, car R= 10 Ohms).
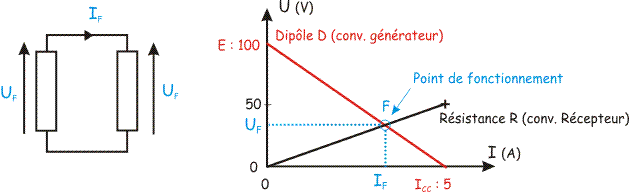
Le point
de fonctionnement (courant qui circule et tension aux borne de la résistance) a
pour coordonnées : UF= 33 V et IF = 3,3 A.
Réponse
donnée par Loïc QUINET le 12 novembre à 17h36 (1 point de bonus sur l'interro 4).
Loïc est hors-jeu jusqu'au 28 novembre.
Question 2
Un
dipôle actif linéaire D présente une caractéristique électrique qui passe par
les points A (225 V; 3 A) et B (165 V; 5 A). Quelles sont les valeurs de la
tension à vide, de l'intensité de court-circuit du dipôle et de la résistance
interne du dipôle D
?
Le plus
simple, si on ne veut pas se lancer dans la résolution de deux équations à deux
inconnues, c'est de travailler sur la caractéristique.
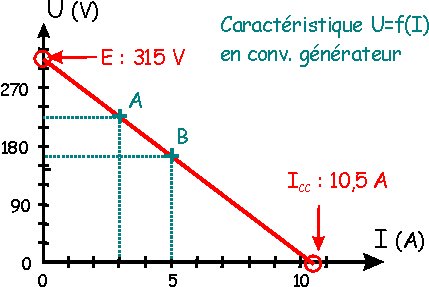 |
|
Après avoir placés les
points A et B, on trace la caractéristique de ce dipôle actif linéaire.
On relève E = 315 V et ICC
= 10,5 A.
La résistance interne, r, se
calcule alors par la relation r= E/ICC
Soit r= 315/10,5 = 30 Ohms.
|
Réponse
donnée par Maxime WOJTKOWSKI le 12 novembre à 19h30 (1 point de bonus sur l'interro 4).
Maxime est hors-jeu jusqu'au 29 novembre.
Question 3
La tension à vide aux bornes d'un dipôle actif linéaire est de 4 V. Connecté à
une résistance de charge de 6 Ohms, il débite un courant d'intensité 0,5 A.
Quelle sera l'intensité du courant si on remplace la résistance de charge par
une autre de valeur 2 fois plus faible ?
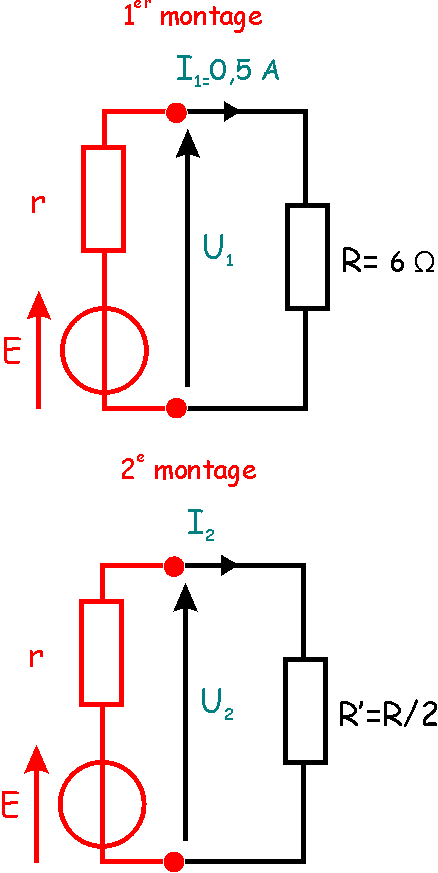 |
|
La tension à vide du dipôle
est de 4V.
Remplaçons ce dipôle actif
linéaire par son M.E.T. et connectons à ses bornes une résistance de charge de 6
Ohms (1er montage). On obtient une maille qui répond à la loi :
Ur + UR
- E = 0. Les éléments r et R étant des résistances, on peut leur appliquer la
loi d'Ohm, à savoir : Ur = r I1 et UR= RI1.
On peut donc écrire rI1 + RI1 - E = 0.
Cherchons r : rI1
= E - RI1 et finalement, r = (E - RI1)/I1 = (4
- 6.0,5)/0,5 = 2 Ohms.
Connectons maintenant aux
bornes de ce dipôle une résistance R' = R/2 = 3 Ohms (2e montage).
La loi de la maille devient
alors : rI2 + R'I2 - E = 0.
Cherchons maintenant I2
: (r + R') I2 = E et finalement I2 = E/(r + R')= 4/(2+3)
I2= 0,8 A.
|
Réponse
donnée par Miguel HERBICH le 2 décembre à 17h52 (1 point de bonus sur l'interro 5).
Miguel est hors-jeu jusqu'au 12 décembre.
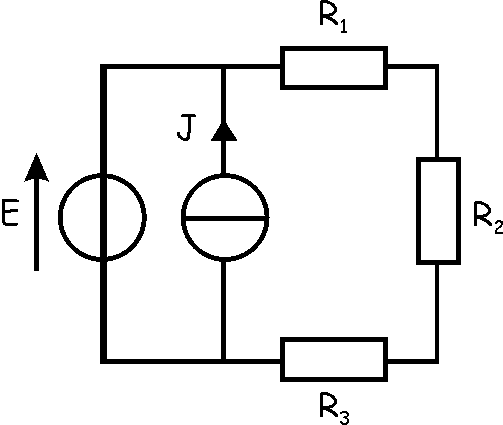 |
|
On donne E= 15 V, J= 3 A, R1=
5 Ohms, R2= 5 Ohms, R3= 5 Ohms.
Calculer la tension aux
bornes de R2.
|
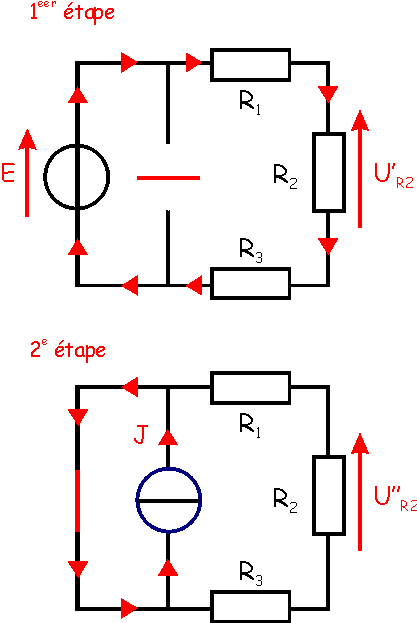 |
|
1ère étape :
On laisse la source de tension allumée, on éteint la source de courant :
La source de courant éteinte
crée un circuit ouvert, tout le courant circule dans les 3 résistances alors
associées en série. On applique le diviseur de tension :
U'R2= (R2/(R1
+ R2 + R3))E = (5/(5+5+5))15 = 5 V
2e étape : On
laisse la source de courant allumée, on éteint la source de tension :
La source de tension éteinte
crée un court-circuit, tout le courant circule dans ce court-circuit, aucun
courant ne parcourt les 3 résistances, donc, d'après la loi d'Ohm:
U''R2= R2.
0 = 0 V
3e étape : On
applique le principe de superposition :
UR2= U'R2
+ U''R2 = 5 + 0 = 5 V
|
Réponse
donnée par Loïc QUINET le 2 décembre à 20h59 (1 point de bonus sur l'interro 5).
Loïc est hors-jeu jusqu'au 13 décembre.
Question 5
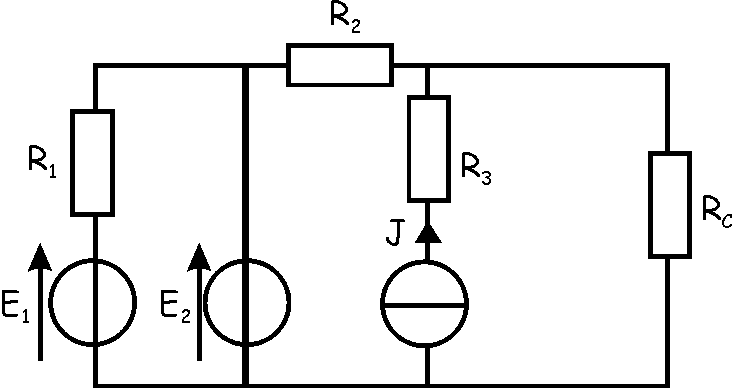 |
|
On donne E1= 20 V,
E2= 10 V, J= 3 A, R1=
10 Ohms, R2= 10 Ohms, R3= 10 Ohms et RC= 20
Ohms.
Calculer la tension aux
bornes de RC.
|
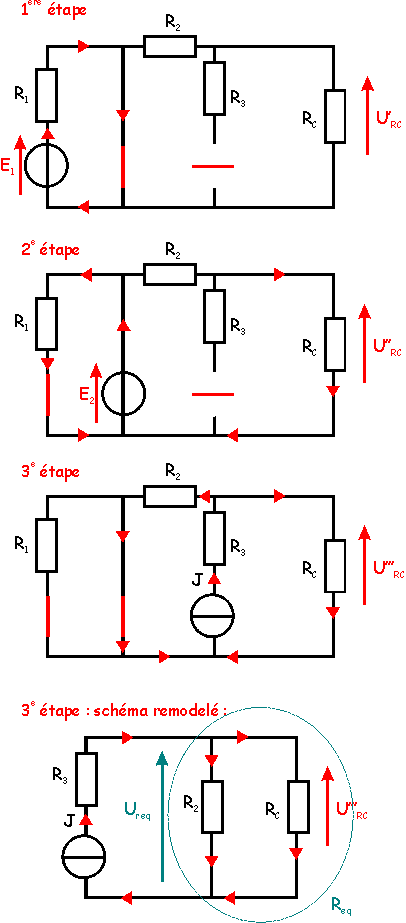 |
|
1ère étape :
On laisse la source de tension E1 allumée, on éteint la source de
tension E2 et la source de courant :
La source de tension E2 éteinte
crée un court-circuit, aucun courant ne circule dans R2 et RC.
Donc, d'après la loi d'Ohm:
U'RC= RC.
0 = 0 V
2e étape : On
laisse la source de tension E2 allumée, on éteint la source de
tension E1 et la source de courant :
On voit que R2 et
RC sont en série, et que l'ensemble est relié à la source de tension
E2. On obtient donc un diviseur de tension.
U''R2= (RC/(R2
+ RC))E2 = (20/(20+10))10 = 6,67 V
3e étape : On
laisse la source de courant allumée, on éteint les deux sources de tension :
On voit que R2 et
RC sont en parallèle. Elles forment une résistance équivalente Req
= (R2 x RC)/(R2 + RC) = (10 x
20)/(10 + 20) = 6,67 Ohms.
La tension aux bornes de Req
est aussi celle aux bornes de RC. On applique donc la loi d'Ohm à Req.
(Req est traversée par l'intensité J)
U'''RC = UReq
= Req J = 6,67 x 3 = 20 V
4e étape : On
applique le principe de superposition :
URC= U'RC
+ U''RC
+ U'''RC= 0 + 6,67 + 20 = 26,7 V
|
Réponse
donnée par Maxime WOJTKOWSKI le 12 décembre à 21h26 (1 point de bonus sur l'interro 5).
Maxime est hors-jeu jusqu'au 23 décembre.
Question 6
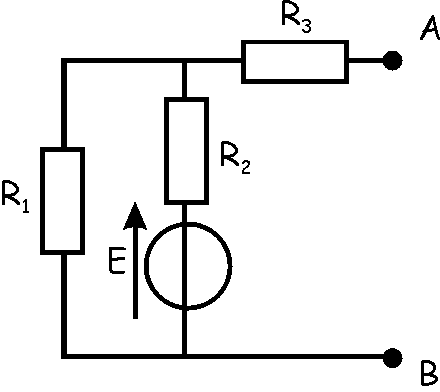 |
|
Déterminer les éléments du
Modèle Equivalent de Thévenin du dipôle AB, constitué par le circuit ci-contre.
On donne E= 20 V, R1=
10 Ohms, R2= 20 Ohms, R3= 30 Ohms .
|
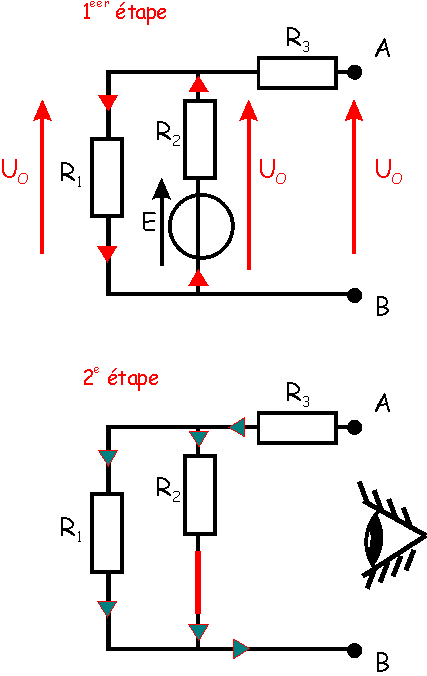 |
|
1ère étape :
Calcul de la tension à vide du dipôle AB :
Le dipôle est à vide (rien
de connecté entre ses bornes A et B), aucun courant ne passe par A, donc aucun
courant ne traverse R3. La tension à vide est donc celle qu'on
retrouve aux bornes de E en série avec R2 ou aux bornes de R1.
Comme R1 et R2 sont en série dans cette maille, nous
pouvons appliquer le diviseur de tension :
UO= UR1= (R1/(R1
+ R2)E = (10/(10+20))20 = 6,67 V
2e étape :
Calcul de la résistance interne du dipôle AB :
On considère encore le
dipôle à vide, et on éteint la source de tension. Celle-ci est alors remplacée
par un court-circuit.
On calcule la résistance vue
de la sortie (entre les points A et B). Un courant entrant par A verrait la
résistance R3 puis, en série avec cette résistance, le groupement
parallèle formé par R1 et R2.
On en déduit donc :
R0 = R3
+ (R1R2)/(R1
+ R2) = 30 + (10 x 20) / (10 + 20)= 36,7 Ohms.
|
Réponse
donnée par Maxime WOJTKOWSKI le 26 décembre à 14h44 (1 point de bonus sur l'interro 5).
Maxime est hors-jeu jusqu'au 5 janvier.
Question 7
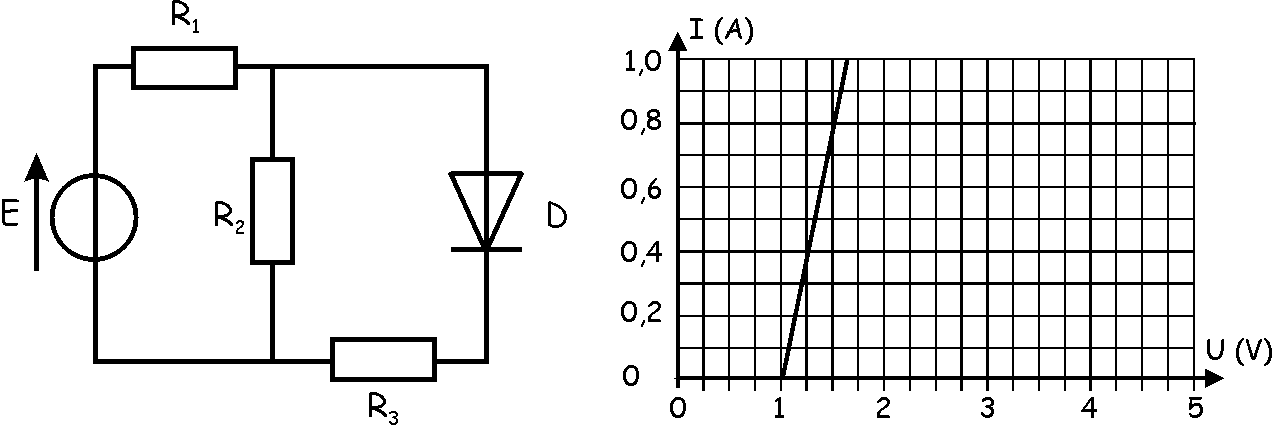 |
|
Déterminer la valeur de la
puissance dissipée dans la diode, dont la caractéristique I=f(U) est donnée
ci-contre.
On donne E= 10 V, R1=
20 Ohms, R2= 20 Ohms, R3= 10 Ohms .
|
|
Les dipôles E, R1, R2 et
R3 sont tous linéaires, on peut donc leur associer un M.E.T. (Théorème de
Thévenin)
1ère étape :
Calcul de la tension à vide de ce dipôle équivalent :
On considère ce dipôle à
vide (rien de connecté à ses bornes) et on calcule la tension à sa sortie. Comme
aucun courant ne peut circuler dans R2, on a UR3 = R3x0 = 0 . La tension à vide
est donc égale à celle aux bornes de R2. Dans cette 1ère étape, R1 et R2 se
retrouvent en série et cette association série est soumise à la tension E : On
peut appliquer le diviseur de tension :
U0= (R2/(R2
+ R2))E = (20/(20+20))10 = 5 V
2e étape :
Calcul de la résistance interne de ce dipôle équivalent :
On éteint la source de
tension E qui devient alors un court-circuit. Vu de la sortie, la résistance
interne correspond à celle du groupement parallèle de R1 et R2, le tout en série
avec R3. Donc :
R0 = (R1R2)/(R1
+ R2) + R3 = (20 x 20)/(20 + 20) + 10 = 20 Ohms.
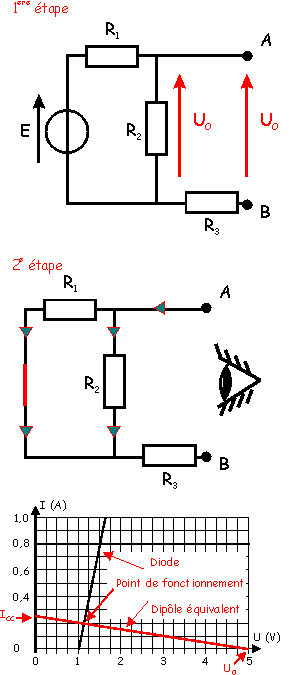
On peut maintenant
tracer la caractéristique de ce dipôle. On lui choisira la convention
générateur, car ce dipôle alimente la diode.
Le plus simple est de
calculer l'intensité de court-circuit de ce dipôle : ICC= U0/R0
= 5/20 = 0,25 A.
On place donc U0
et ICC, puis la droite caractéristique équivalente au M.E.T.
On en déduit maintenant
graphiquement le point de fonctionnement, c'est à dire la tension et l'intensité
concernant la diode :
UF = 1,12 V et IF
= 0,2 A
Il ne reste plus qu'à en
déduire la puissance absorbée par la diode :
P = UF.IF
= 1,12 x 0,2 = 224 mW
|
|
|
Réponse
donnée par Loïc QUINET le 12 janvier à 17h13 (1 point de bonus sur l'interro 6).
Loïc est hors-jeu jusqu'au 23 janvier.
Question 8
|
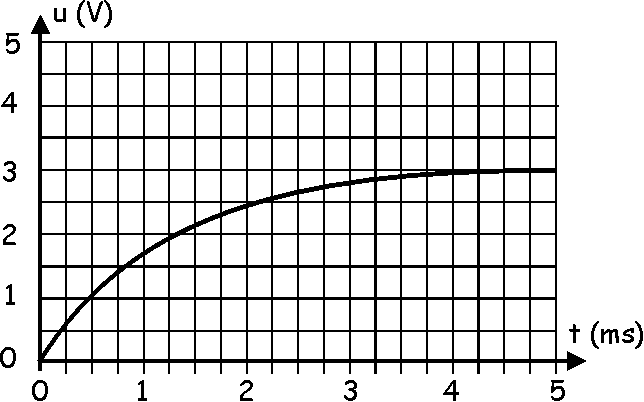
Un condensateur voit sa
tension u évoluer au cours du temps comme indiqué sur le graphe ci-contre. A t=
2 ms, un capteur mesure l'intensité du courant qui arrive au condensateur : 5
µA. Quelle est la valeur de la capacité de ce condensateur ?
|
|
|
 |
|
La relation liant i à u pour
un condensateur est i = C du/dt.
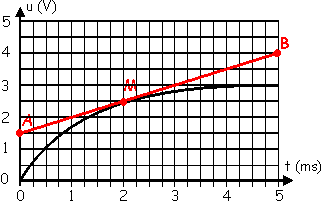
Nous nous intéressons au
point M de la courbe correspondant à t = 2 ms. On trace la tangente à la courbe
à la courbe en M. La dérivée en M (c'est à dire pour t = 2 ms) correspond au
coefficient directeur de la tangente en M.
Prenons deux points A et B
sur cette tangente.
du/dt = ( UB - UA
) / ( tB - tA ) = ( 4 - 1,5 ) / ( 5.10-3 - 0 )
= 500 V.s-1
On a alors C = i / ( du/dt )
= 5.10-6 / 500 = 1.10-8 F
On trouve C = 10 nF.
|
Réponse
donnée par Maxime WOJTKOWSKI le 14 janvier 16h56 (1 point de bonus sur l'interro 5).
Maxime est hors-jeu jusqu'au 25 janvier.
Question 9
|
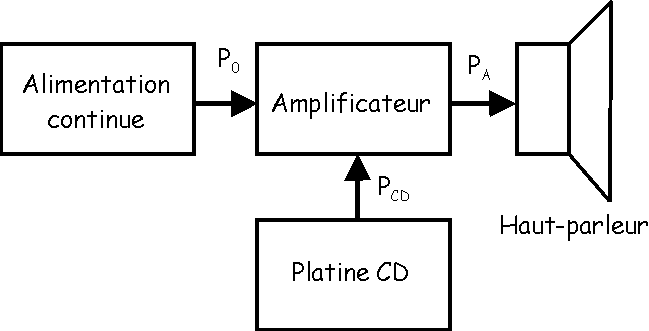
Pour un fonctionnement
donné, l'amplificateur fournit au haut-parleur une puissance électrique PA
= 50 W avec un rendement de 60 %. La puissance PCD fournie par la
platine CD est négligeable.
Le haut-parleur transforme
la puissance électrique en puissance acoustique avec un rendement de 70 %. Quel
est le rendement de l'ensemble de l'installation ?
|
|
|
Exprimons chacune des
puissances : rendement(ampli) = Pu (ampli) / Pabs
(ampli) = PA / ( PO + PCD) =
PA / PO car PCD est négligeable.
Donc PO =
PA / rendement(ampli) = 50 / 0,6 = 83,3 W
La puissance acoustique
répond à la relation : rendement(HP) = Pu (HP)
/ Pabs (HP) = Pacoustique / PA.
Donc Pacoustique
= rendement(HP) x PA = 0,7 x 50 = 35 W.
L'installation complète a
un rendement tel rendement(installation) = Pu
(installation) / Pabs (installation) = Pacoustique /
( PO + PCD) = Pacoustique / PO.
rendement(installation) = 35 / 83,3 = 0,42 soit 42 %.
Réponse
donnée par Maxime WOJTKOWSKI le 25 janvier 11h19 (1 point de bonus sur l'interro
6).
Maxime est hors-jeu jusqu'au 5 février.
Question 10
La force
électromotrice d'un électromoteur réversible est E = 70 V. Lors d'un
fonctionnement en récepteur, il est traversé par un courant d'intensité I est
absorbe une puissance P = 1176 W. Pour qu'il fournisse une puissance utile égale
à p quand il fonctionne en générateur, il faut lui faire débiter un courant
d'intensité double du précédent, soit 2 I.
Calculer la résistance
interne de cet électromoteur.
Quand le dipôle actif
linéaire est récepteur, il absorbe une puissance P1 = U1
.I avec U1 = E + rI donc P1 = (E + rI).I
Quand le dipôle actif
linéaire est générateur, il fournit puissance P2 = U2 .I
avec U2 = E - rI donc P2 = (E - rI).I
Or, on a des puissances
égales si on considère le dipôle récepteur avec une intensité qui vaut I et si
on le considère générateur avec une intensité qui vaut 2I, donc :
(E + rI).I = (E - r(2I)).2I
= (E - 2rI).2I
On peut simplifier par I de
chaque côté, ce qui donne : E + rI = (E - 2rI).2 = 2E - 4rI
En mettant les rI à gauche
et les E à droite du signe égal, on obtient : rI + 4rI = 2E - E
soit 5rI = E
d'où rI = E/5 = 70/5 = 14 V.
En reprenant une des deux
puissances au départ, on a P1 = (E + rI).I soit I = P1
/(E + rI) = 1176 / (70 + 14) = 14 A.
Comme rI = 14 V, on a
finalement r = 14/I = 14/14 = 1 Ohm
Réponse
donnée par Maxime WOJTKOWSKI le 25 mars 17h11 (1 point de bonus sur l'interro 8).
Maxime est hors-jeu jusqu'au 5 avril.
Question 11
|
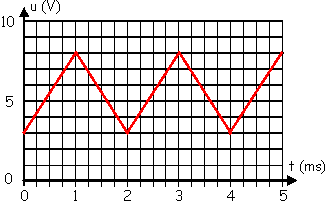
On mesure le signal ci-contre avec un
multimètre numérique en fonctionnement voltmètre. On a sélectionné la fonction
AC+DC.
Quelle valeur indique le multimètre ?
|
|
|
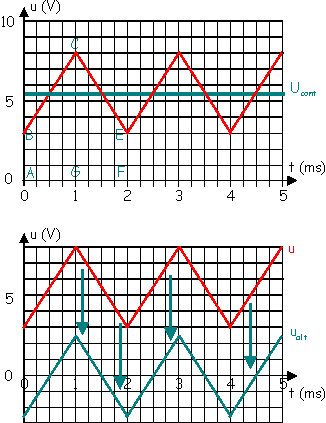 |
|
1ère étape :
Détermination de la composante continue de u :
On pourrait appliquer la
méthode des aires en considérant soit les trapèzes ABCG et CEFG, soit le
rectangle ABEF et le triangle BEC.
Cependant, le signal étant
triangulaire, la valeur moyenne se situe au milieu de la valeur maximale et de
la valeur minimale, donc :
ucont = < u > = ( umax
+ umin ) / 2 = ( 8 + 3 ) / 2 = 5,5 V
2e étape :
Détermination de la composante alternative de u :
Par définition, on décompose
le signal périodique en la somme de ces deux composantes, à savoir :
u = ucont + ualt
d'où ualt = u - ucont
finalement ualt = u - 5,5
Pour tracer ualt
il suffit d'enlever 5,5 V à chaque valeur de u.
ualt est donc un
signal alternatif triangulaire d'amplitude 2,5 V.
3e étape :
Détermination des valeurs efficaces :
- ucont est un
signal continu donc Ucont = ucont = 5,5 V.
- ualt est un
signal triangulaire alternatif donc Ualt = Ûalt / V3 = 2,5
/ V3 soit Ualt = 1,44 V (voir exemples dans le chapitre "valeur
efficace").
- La valeur efficace d'un
signal périodique se déduit de celles de sa composante continue et de sa
composante alternative (voir DS7) par la relation : U² = ucont² + ualt².
Donc U = V ( ucont²
+ ualt² ) = V ( 5,5² + 1,44² ) = 5,69 V
|
Réponse
donnée par Maxime WOJTKOWSKI le 19 avril à 11h53 (1 point de bonus sur l'interro
9).
Maxime est hors-jeu jusqu'au 30 avril.
Question 12
Un générateur basses
fréquences alimente un circuit série constitué d'une résistance R de 100 Ohm,
d'une inductance L de 100 mH et un condensateur C de 1,6 µF. Le G.B.F délivre
une tension u de valeur efficace 10 V et de fréquence 500 Hz. Donner la valeur
efficace de l'intensité qui parcourt ce circuit ainsi que le déphasage de
l'intensité par rapport à la tension du G.B.F. (préciser si i est en avance ou
en retard sur u).
1ère étape :
Calcul des différentes impédances des dipôles récepteurs :
- L'impédance complexe de la
résistance vaut [ R ; 0 ] = R soit ici ZR = [ 100 ; 0 ] = 100
Ohms
- L'impédance complexe
de l'inductance vaut [ L w ; 90° ] = j L w soit ici ZL = [
100.10-3 x 2 pi x 500 ; 90 ° ] = [ 314 ; 90° ] = j 314 Ohms.
- L'impédance complexe
du condensateur vaut [ 1 / C w ; -90° ] = - j / C w soit ici ZC = [
1 / 1,6.10-6 x 2 pi x 500 ; -90 ° ] = [ 199 ; -90° ] = -j 199 Ohms.
2e étape :
Calcul de l'impédance totale relative aux trois dipôles en série :
Les trois dipôles
élémentaires étant associés en série, l'impédance complexe totale est égale à la
somme des impédances complexes de chaque dipôle :
Z = ZR + ZL
+ ZC = 100 + j314 - j199 = 100 + j115 soit en représentation
trigonométrique : [ V 100² + 115² ; Arctan ( 115/100) ]
Z = [ 152 ; 49° ]
3e étape :
Calcul de l'intensité :
Aux bornes de l'ensemble, on
a donc U = Z I soit I = U / Z. En prenant u comme référence des phases, on
obtient :
I = [ 10 ; 0 ] / [ 152 ; 49°
] = [ 0,0658 ; -49° ].
L'intensité dans le circuit
a donc une valeur efficace de 65,8 mA et elle est en retard de 49° sur u
(puisqu'on a pris u comme référence des phases).
Réponse
donnée par Maxime WOJTKOWSKI le 30 avril à 15h39 (1 point de bonus sur l'interro
9).
Maxime est hors-jeu jusqu'au 11 mai.
Question 13
Un générateur basses
fréquences délivre une tension de valeur efficace 5 V qui alimente un circuit série constitué d'une résistance R de 100 Ohm,
d'une inductance L de 100 mH et un condensateur C de 1,6 µF. Donner la valeur
maximale que peut prendre la valeur efficace de l'intensité du courant qui
parcourt ce circuit ainsi que la fréquence pour laquelle on obtient cette valeur
maximale.
1ère étape :
Tension délivrée par le G.B.F. :
On considère que le G.B.F.
délivre une tension dont la valeur efficace est constante, quelle que soit la
fréquence. Appelons la U.
2e étape :
Intensité du courant appelé par la charge :
Si c'est le G.B.F. qui
impose la tension aux bornes du circuit, c'est bien la charge qui impose le
courant dans le circuit.
On a donc U = Z
I d'où I = U / Z
Comme on ne s'intéresse qu'à la valeur maximale de
l'intensité efficace, on n'a pas besoin des arguments, on peut donc travailler
uniquement sur les modules et écrire : I = U / Z.
Comme U est constante quelle que soit la fréquence, on
aura forcément la plus grande intensité efficace pour la plus petite valeur
d'impédance.
On aura donc I = Imax quand Z = Zmin,
pour avoir : Imax = U / Zmin




















